ORIGAMI "HIPERPURISTA"

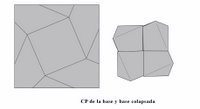
En teoría no existe nada llamado así pero en la práctica hay un origami que no tiene dobleces estimados, tiene casi únicamente dobleces con ángulos múltiplos de 22,5° (o de 15° llegado el caso), y se limita a unos pocos pasos de terminación, tal vez tres o cuatro pero a veces uno o ninguno.
Al no tener casi pasos de terminación, el patrón de dobleces colapsado ES prácticamente el modelo, factor que los amantes de estos rompezabezas de una sola pieza agradecen.
Este tipo de modelos tienen un aspecto bastante característico, pero al contrario de lo que podría pensarse no son necesariamente rectos, rígidos y sin vida. El concepto subyacente es que cualquier cosa que se quiera expresar en el modelo tiene que poder ser hecha usando dobleces "exactos" y que no hace falta nada más.
No estoy diciendo que todo el origami deba ser así. Estoy reconociendo la existencia de un estilo que me resulta muy atractivo y que ha dado algunas de las mejores obras de todos los tiempos. En el caso del buho de Komatsu por ejemplo queda demostrado que incluso la tridimensionalidad se puede lograr usando únicamente este tipo de ángulos y muy poca terminación (el modelo se torna 3D casi sobre el final del diagrama ¡en un sólo paso de terminación!)

Voy a llevar esto un poco más lejos. Con las tres condiciones que tenemos para el estilo no puedo dejar de pensar... en el origami tradicional (por supuesto que en el origami tradicional se usaban cortes, pero los modelos que se salvaban de las tijeras solían tener las "reglas" que describo aquí)
Creo que de alguna manera este origami es (no voy a decir el heredero, pero...) la versión evolucionada en línea recta del origami tradicional purista.
La estructura más compleja aceptada en el origami tradicional era probablemente la base de rana. No es demasiado arriesgado decir que los diferentes niveles de complejidad alcanzados por el origami en la segunda mitad del siglo 20 tienen ese punto de partida (la base de rana)
Desde allí se avanzó hacia muchos lados al mismo tiempo: varios papeles, variedad de angulos, variaciones de las bases tradicionales, dobleces curvos, "box pleating".
Pero de todos, hay un elemento que es necesario entender: lo que cambió fue la unidad de construcción de los modelos. En libros como Creative Origami de Kasahara la unidad para diseñar una pata, rabo o cabeza era una aleta de una base tradicional. La aleta era casi indivisible. El propio Kasahara dice en ese libro que la manera de obtener un animal con cuatro patas es usando dos papeles, uniendo dos bases de pájaro, pero no plantea muy claramente que exista la posibilidad de obtener bases diferentes a las tradicionales adaptadas a un cuadrúpedo.
Para ese entonces ya existían autores como Yoshisawa o Peter Engel que dividían las aletas a gusto inventando métodos para generar gran número de puntas y escapaban así a la dictadura de las bases tradicionales.
Las variaciones "blintz" de las bases tradicionales así como muchas divisiones de puntas tienen exlcusivamene ángulos múltiplos de 22.5 , por lo que la línea del origami tradicional se mantiene pero aumentando el nivel de complejidad.
En el origami "hiperpurista" de hoy ya difícilmente se reconozca alguna base tradicional (y probablemente entonces le llamaríamos "neotradicional" o algo así!)
Este tipo de origami puede alcanzar niveles de complejidad comparables a cualquier otro estilo, pero siguiendo reglas todavía más acotadas que las del, ya de por si acotado, origami.
Me gusta pensar en este estilo como el que ha logrado trasladar la simplicidad de los métodos de las figuras tradicionales y la ha usado para formar estructuras mucho más complejas.
Pero también ha traído algunas formas complejas al origami de muy pocos dobleces. Por eso lo veo como una encrucijada de lo más simple y lo más complejo.
Además diseñar las terminaciones de los detalles de tal manera que tengan determinados ángulos y que sea posible incluirlas razonablemente en el patrón de dobleces es un ejercicio impresionante de control sobre el papel y el proceso de doblado.

Para el que quiera practicar con el patrón de dobleces de un modelo con estas características dejo aquí un ejemplo.
En la entrada anterior de este blog incluí cuatro fotos de modelos que había estado trabajando la semana anterior: tres de ellos son figuras hiperpuristas.
El más complejo de los tres es este Elefante acróbata que tuvo un par de días más de trabajo para llevarlo casi por completo al estilo. El patrón de dobleces tiene sólo una línea (la que forma el borde posterior de las patas delanteras) con un ángulo que no es múltiplo de 22.5 , y una vez colapsadas todas las líneas hay que hacer únicamente un doblez reverso bajando la cola para que la figura quede terminada.

SIMPLE (?)

Debo confesar, siempre quise diseñar simple.
El asunto es que diseñar complicado es mucho más fácil. Los modelos realmente buenos y logrados con unos pocos elementos son un reto mayor para el diseñador.
Por algo Nick Robinson o Hatori Koshiro defienden fieramente lo que hacen. Pero ni siquiera hablo de llegar tan lejos como el minimalismo o el "pureland" sino simplemente de los modelos con pocas líneas, en los que el efecto se logra con una pose o con algún elemento anatómico dominante.
Pero en definitiva ¿qué elementos convierten a un modelo en más simple o más complejo?

Aparentemente es muy fácil darse cuenta cuando algo es complicado o simple.

Existe una escala de complejidad (he escuchado que se le atribuye a Montroll pero no estoy seguro si esto tiene algún fundamento) que habitualmente se usa en los libros de origami. Algunas veces se califica del 1 al 4 y otras del 1 al 5. Se usan nombres como simple, intermedio, complejo y muy complejo y existen muchas versiones del tema (me gusta particularmente una escala que incluye el nivel ¡"intrincado"!)
Pero lo que sistemáticamente falta es un criterio bien explicado de porqué un modelo es evaluado de determinada manera. He seguido varias veces las conversaciones que surgen sobre el tema, especialmente en la "O-list" y sistemáticamente fallan en explicar porqué un modelo debería ser considerado en un punto u otro de la escala de dificultad y ni hablemos de dar algún método objetivo para medirlo. En general se explica, un tanto vagamente, mediante los tipos de dobleces que contiene la secuencia. Existe un límite bien neto marcado por el origami "pureland" en que sólo se admiten los valles y montes, pero el resto del origami cae en una nebulosa mal definida. Una de las pocas cosas que podemos medir objetivamente de un modelo es el aporte de Lang que calcula cuan eficiente matemáticamente ha sido el modelo en el uso del papel, pero esto, por cierto no es una escala de

dificultad (y a mi gusto tampoco necesariamente de calidad, pero eso es otro tema...)

Voy a intentar mencionar una lista de criterios, más o menos medibles, de complejidad (o simplicidad) de modelos de origami y voy a explicarlos brevemente, intentando comprender porqué a veces algo muy sencillo es complicadísimo y viseversa.

1. Número de dobleces.

Una manera simple de objetivar cuanto se ha trabajado sobre un modelo. Por ejemplo el gallito de la foto tiene 25 dobleces diferentes. Sólo he tomado en cuenta los dobleces que permanecen doblados en la figura terminada, por eso los he contado sobre el patrón de dobleces sin tomar en cuenta los pliegues "de construcción".

2. Número y variedad de pasos.

El número de pasos parece ser un criterio obvio y tiene una altísima correlación con la escala clásica de dificultad. Cobra aún más sentido si lo relacionamos con el parámetro anterior e intentamos medir cuantos dobleces se generan en cada paso o dicho de otra manera, la proporción pasos/dobleces.

Yendo a un ejemplo, a veces encontrar un punto en el papel toma 4 o 5 pasos, por lo que aumentaría la relación. Es de notar también que esto suele ocurrir en modelos más complejos, especialmente aquellos con diseño matemático.

Sin embargo la cuenta puede ser engañosa cuando aparecen los pasos repetitivos. Por otro lado sería lógico pensar que un modelo cuyos pasos son todos diferentes es más complejo que uno que

se limita a repetir una y otra vez el mismo movimiento en forma rutinaria.

3. Regularidad y variedad de los ángulos del pátrón de dobleces.

Nuevamente el patrón de dobleces aparece como un elemento en el que se puede medir dificultad. Voy a considerar que los modelos en los que predominan los ángulos múltiplos de 22,5 son más simples que los que tienen predominancia de otros ángulos. Pero también se debería integrar de alguna manera a este criterio la diversidad de ángulos, siendo más complejo cuanto más diversos sean los ángulos.

¿Se adapta este criterio a los modelos hechos por "box pleating"? Creo que si. En términos generales un modelo que contenga solamente ángulos de 90 y 45° no puede ser muy complejo y si resulta serlo será porque tiene un gran número de dobleces y un gran número de pasos por lo que siempre habrá otros criterios que expliquen su dificultad.

Por otra parte estos modelos suelen presentar ángulos de "box pleating" sólo hasta la base pasando luego a tener una mayor variedad de ángulos

4. Número y variedad de elementos diferentes en el modelo terminado.

Mientras que los tres criterios anteriores miden directa o indirectamente la estructura interna del modelo, este por el contrario intenta medir lo complejo del aspecto externo.

Pienso que este criterio es indispensable para explicar algunos modelos "engañosos", cuya apariencia externa tiene pocas particularidades pero por alguna razón se necesitan muchos pasos o muchos dobleces o ángulos muy extraños para lograr ese aspecto aparentemente fácil.

Como "elementos diferentes" se pueden considerar desde los cambios de color hasta la variedad del largo de los apéndices de un insecto (por algo el escorpión "varileg" se llama así, y es mucho más complejo que el escorpión con patas de largo regular) pero también se deben considerar los planos, adornos y cualquier cosa que está representada en el papel. Si vemos un caso como el de la carpa con escamas de Lang tedremos 900 elementos representados (gran dificultad) pero no diferentes, si las escamas fueran diferentes, como en el pangolín de Joisel o el Arawana de Cheng Chit, la dificultad sería mucho mayor aun.

5. Linearidad de la secuenciade doblado.

En lugar de hablar de los tipos de dobleces considerados difíciles que presenta la secuencia (hundidos, dobles reversos, etc) prefiero tomar en cuenta cuan lineal resulta el método. El tiempo (medido en pasos) que el modelo permanece en forma tridimensional aumenta la dificultad del doblado. Una secuencia en que cada paso comienza y termina en un plano es notoriamente más sencilla.

Muchas veces los dobleces "3D" se usan para "ahorrar" pasos 2D por lo que una secuencia puede aparecer como artificialmente corta; tomando en cuenta el criterio de linearidad se compensa el artificio.

6. Número de dobleces de terminación.

En el mundo ideal las terminaciones comienzan donde termina lo que puede razonablemente ser representado en el patrón de dobleces. No es siempre el caso ni mucho menos pero como criterio general y tomado con cierta flexibilidad me parece válido.

Una gran cantidad de dobleces de terminación (a veces "no formales", con proporciones estimadas, etc) generalmente se consideran como un factor que dificulta un modelo. Los modelos humanos de Hojyo (¡que satisfacen todos los criterios de alta dificultad aquí enumerados!) suelen tener (por si fuera poco) una gran cantidad de terminaciones luego de las base haciéndolos todavía más difíciles.

Pero este criterio me gusta también para explicar fenoménos "raros" del origami que aparentemente no se adaptarían a esta lista como son las máscaras de Joisel o los obras de Giang Dinh. Estos modelos resultan estar constituidos prácticamente sólo por "terminaciones" desde el comienzo.

Entonces tienen pocos dobleces (simple) , pocos pasos (simple), a veces pocas partes diferentes (simple), pero la variedad de ángulos "raros" y sobretodo el hecho de estar construidos casi enteramente mediante dobleces informales y de tener una gran cantidad de pasos 3D los puede convertir en complejos (pero probablemente NO "supercomplejos" debido a la falta de los otros elementos)

..............................................................................................................................................................

¿Vale la pena fabricar una complicada escala de dificultad con estos 6 puntos?

Francamente no lo creo, pero me resultan muy útiles para describir el tipo de modelo del que estamos hablando y caracterizar donde reside su dificultad.

Tomemos por ejemplo un modelo como el famosísimo león de Komatsu. No existe por ahora una secuencia de doblado publicada para el modelo y cualquier intento por diseñarla termina dando muchos pasos en 3D, demasiados para dibujar un diagrama razonable, eso es aparentemente su mayor dificultad, pero también el número de dobleces en el patrón de dobleces es altísimo. Tiene sin embargo elementos que lo hacen menos complicado que otros modelos: la regularidad de los ángulos y un mínimo de pasos de terminación.

Es interesante ver como Komatsu ha convertido la regularidad de los dobleces y el mínimo posible de pasos de terminación casi en una premisa comparable quizás a las reglas del "pureland". Estas dos particularidades de sus modelos es lo que los mantiene alejados de la supercomplejidad que "deberían tener" de acuerdo a otros parámetros, incluyendo la cantidad y variedad de elementos representados, como las rayas del tigre, el lomo del lobo o las plumas de águila.

De manera similar muchos diseños de insectos tienen un patrón de dobleces bastante regular en sus ángulos pero una enorme cantidad de dobleces, pasos y apéndices representados los convierten en complejos.

Aparentemente es difícil diseñar modelos en los que todos los criterios tiendan al máximo de complejidad como Yoshino Issei en su "supercomplex origami"

El camino más común es mantener uno o dos criterios dentro de lo sencillo para poder complicar otros.

Por ejemplo en el diseño de mi Hipocamppus representé muchos elementos y cada uno muy diferente al otro, pero no fui muy arriesgado en los ángulos pues predominan los múltiplos de 22,5.

De la misma manera podemos considerar el uso de ángulos poco comunes si mantenemos bajo el número de dobleces; es muy difícil seguir doblando con lógica por demasiados pasos si no tenemos algún ángulo conocido en el que apoyarnos.

Los modelos no pueden ser calificados como simples o complejos tomando en cuenta uno o dos parámetros solamente. Hay una variedad de cosas que los empujan hacia la sencillez o la complicación. En general uno de esos elementos pesa más que los otros para un determinado modelo y es en base a este elemento que será calificado. Los modelos que por alguna razón "deben" ser muy complicados (supongamos un erizo de mar) tienen que resolver parte del problema de una manera muy simple (supongamos dobleces repetitivos y ángulos regulares) pues de otra manera se convertirían en tan complejos que no podrían ser ni siquiera diseñados.

Cada autor decide de acuerdo a su naturaleza y criterio estético que parámetro sacrificar hacia la simplicidad y cual complicar.

Finalmente llego (un poco apresuradamente) que estos parametros pueden también ser usados hasta cierto punto como criterios de "calidad" más amplios que la constrictiva "eficiencia del uso del papel". En este sentido podemos pensar cuan bien se prestan unos parámetros al servicio de otros. ¿Cuantos dobleces se necesitaron para representar tales o cuales elementos? o ¿son los ángulos innecesariamente irregulares? o ¿podría lo mismo ser hecho son una secuencia plana?

Y todo tiene sentido partiendo del postulado que en el origami, más simple es mejor y que no intentamos hacer las cosas difíciles sin un propósito que valga la pena.

ORIGAMI QUE GIRA

Cuando nos enfrentamos al famoso cuadrado de papel solemos considerar dos tipos de simetría: la diagonal y la paralela al borde. Es siempre emocionante saber cual vamos a usar para determinado diseño pues es una de las primeras grandes decisiones técnicas de diseño que hay que hacer, y no siempre le acertamos de primera.
Podríamos considerar una tercera forma de simetría que es justamente la asimetría e incluso una cuarta : la simetría radial. Este tipo de simetría le da el mismo tratamiento a las cuatro puntas y/o a los cuatro bordes del cuadrado. Cualquier flor de origami con ocho pétalos tiene simetría radial (como el lirio tradicional por ejemplo)
Pero se me dió por pensar en la simetría radial rotada 22.5 grados, es decir que no sólo la simetría es radial sino que "gira" hacia un lado u otro como una hélice.
Por un lado la primera figura del blog de Andrés Sanchez y por otro la rotación de la mano de Komatsu me recordaron una base que tenía olvidada en un cajón.
Se la mandé hace tiempo a Daniel Naranjo con el nombre de "semi blintz rotado" y este mismo dibujo, con la esperanza que él le pudiera encontrarle el uso que yo no había podido. Pero la base resultó tan inútil que se le sacaba más jugo a un ladrillo.
Por supuesto que al igual que un blintz común, lo mismo puede hacerse con una base pez o cualquier otra base tradicional.
Al hacer la base no se puede evitar pensar en un
blintz pero sería mucho más interesante ver a toda esta familia de bases como injertos radiales. Empezamos con una base conocida y le agregamos partes de tal manera que resulte un cuadrado más grande.

Aquí está como se forman estas bases si las consideramos como injertos.

En este segundo intento de darle un uso a la idea pensé en hacer un aparato volador. Estas bases son evidentemente giratorias así que surgió una especie de dardo giratorio a partir de una base en la que el injerto radial era más ancho que en la base anterior. La referencia es la de una base de cometa.
Lo más atractivo de esta base es que al doblarla hay que ir rotando el papel 90° sobre su eje prácticamente luego de cada paso. Es decir que en lugar de los clásicos "dar vuelta" o "repetir atrás", las repeticiones son radiales, dando la sensación giratoria desde el doblado de los primeros pasos hasta llegar al modelo volador mismo.
Así quedó el patrón de doblaces de la figura a partir de esta base. El cuadrado central aloja una base de rana y el papel injertado sirve para formar las aletas del dardo. Como pasa a veces con el "origami con uso" tiene requerimientos poco comunes de papel (un vaso de origami debe ser doblado con papel encerado por ejemplo) Funciona mejor cuando se dobla con papel fino y pesado como es el metalizado. Para compatibilizar lo pesada que debe ser la punta con lo liviano de las aletas no hay más que recurrir a la acumulación de capas y la base de rana cumple con este propósito. Muchos aviones de papel doblan dos o tres capas de más en la punta con el mismo propósito. Esto claramente contradice el criterio general de "menos capas es mejor" o "eficiencia = elegancia". Y nos lleva directamente a otro tema que es el de los usos del papel , talvez para tratar otro día. Por ahora que quede la idea de que el cotrapeso puede ser un uso perfectamente válido del papel tanto para el "origami con uso" como para el "origami representativo"

Enseñé este modelo ayer, en la reunión mensual de Origami de Calgary. Es sorprendente cuanto más atractivo puede ser un modelo que al terminarlo se puede lanzar de un lado al otro del salón si lo comparamos con un modelo que se queda quieto en una mesa!

DOS DE HISTORIETA y un secreto....

Esta me manda Meri Afranchinno de Rosario Argentina

Y esta encontré de casualidad

Vuelvo a lo mismo: cada uno su propio origami.

El "linyera" de Tabaré mira el barquito y se imagina una cena de merluzas!

Y cada uno su origami, algunos dicen "cosas de pajaritas"....